Géométrie

Présentation du cours:

La notion d’un espace affine. C’est un ensemble de points, il contient des droites, des plans et la géométrie affine discute, par exemple, des relations entre ces points et ces droites (points alignés, droites parallèles ou concourantes...). On définit ensuite la notion de barycentre, issue de la mécanique, y joue un rôle essentiel. Nous étudierons ensuite les applications affines Ce sont celles qui conservent les barycentres. Leur importance vient de ce que la quasi-totalité des transformations géométriques que vous avez pu rencontrer, en particulier les isométries et plus généralement les similitudes, sont affines...

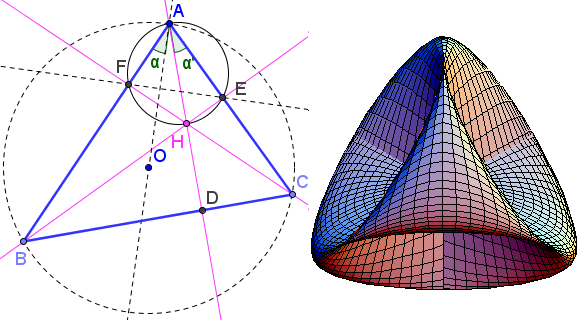
Paramétrisation des courbes et des surfaces

Objectifs:

• Acquérir les bases de la géométrie affine et de la géométrie euclidienne.

• Maîtriser la géométrie des courbes paramétriques.